← TEMPERATURE →

Rayleigh-Bénard convection is a type convection driven by a temperature difference between the top and bottom boundaries of the fluid's container. Click, drag, and RELEASE the slider to change the temperature difference (ΔT) and see how the fluid's flow changes. The Rayleigh number depends on ΔT, gravity, the height of the container, the viscosity of the fluid, and the thermal diffusivity of the fluid. Low Rayleigh numbers indicate weaker convection, and higher Rayleigh numbers indicate stronger, more intense convection.
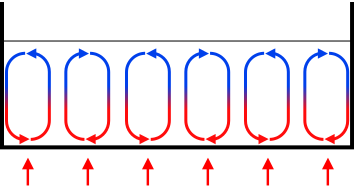
Rayleigh-Bénard convection is a buoyancy-driven flow in a container with a temperature gradient. As the fluid at the bottom heats up, its density decreases, so buoyant forces push the less-dense fluid up towards the cooler end of the container. Meanwhile, the cooler fluid at the top is denser, so it sinks and displaces the warmer fluid. There is a continuous density gradient, and this cyclical motion creates Bénard convection cells. Rayleigh-Bénard convection is one type of natural convection, since it is not propelled by an outside force.
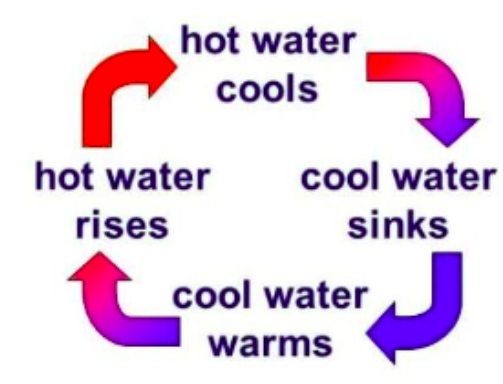
Why does hot water rise? Why does cool water sink?
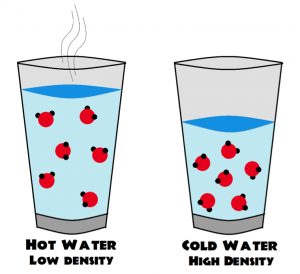
Warm water is less dense than cool water, and thus it has less mass. The buoyancy force pushes the less-dense, warmer water upward because this upward force is greater than the force (from the weight of the water) directed downwards.
Why is hot water less dense than cooler water?
Hotter particles have more kinetic energy, so they bounce around faster and thus have more empty space between them.
Researchers use the Rayleigh number to measure the “amount of convection” in a flow. This number helps researchers compare results between experiments conducted with differently sized containers and different fluids. Fluids with a Rayleigh number below 1708 are not convective; heat moves through the fluid only by conduction among the molecules. The molecules are not moving yet. At Ra = 1708, laminar convection begins. Laminar means that the layers of fluid in the convection cells are not interfering with each other; the flow is "smooth". At high Rayleigh numbers, Rayleigh-Bénard convection is a turbulent flow, which means that the fluid layers are interfering with each other.
This is how the Rayleigh number is defined:
$$Ra = \frac{\alpha g \Delta T H^{3}}{\nu \kappa}$$
where:
\(\alpha\) = thermal expansion coefficient
\(g\) = acceleration due to gravity
\(\Delta T\) = temperature difference between the top and bottom boundaries
\(H\) = thickness of the fluid layer
\(\nu\) = kinematic viscosity of the fluid
\(\kappa\) = thermal diffusivity of the fluid
The particular animated experiment above used values for a cylindrical tank that was 10 cm tall, filled with water starting at 20°C:
\(\alpha = 2.07 \times 10^{-4} \frac{1}{K}\)
\(g = 9.8 m/s^2\)
\(\Delta T\) = from slider value
\(H= 0.01m\)
\(\nu= 1.0023 \times 10^{-6} m^2/s\)
\(\kappa=0.143 \times 10^{-6} m^2/s\)
As you can see from the animation, turbulent convection can get very complicated very quickly. Turbulence is chaotic, which means that a very small change in the initial conditions can have a huge impact on the future flow of the system. Turbulence is often labeled as one of the last unsolved problems in classical physics. Physicists usually use equations to model systems in the real world, and we have the Navier-Stokes equations to describe the motion of viscous fluids, but it has not yet been proven if solutions always exist to these equations. This is why researchers are trying to study turbulence using machine learning models like reservoir computing.
Rayleigh-Bénard convection is everywhere—in our atmosphere, our oceans, the Earth's mantle, and even on other planets. Studying convection can help us gain a better understanding of these geophysical systems that rely on Rayleigh-Bénard convection. For instance, the Earth's atmosphere is made of gases, and convection in the ocean drives the wind patterns, which have a significant influence on our day-to-day weather. Understanding convection—especially turbulent convection—can improve our understanding of weather patterns and predictions.
Notice that we held all the values constant for this specific animation. Rayleigh-Bénard convection can produce very interesting patterns with fluids of different viscosities and different heights.

A movie from an experiment using a thin layer of compressed gas:
A very colorful and turbulent (high Ra) simulation of Rayleigh-Bénard convection:
Created by Sarah Chang
TREND REU Media Project, Summer 2019