Plasma turbulence

Turbulence is ubiquitous in plasmas, just as it is in non-conducting gases and liquids. Plasma turbulence has features not found in other types of turbulence: velocity-space effects are often important, magnetic fields introduce strong anisotropy, and natural length scales like the gyroradius are significant. Turbulence causes transport of heat out of hot fusion plasmas, similar to a boiling pot of water on a stove, with convective cells carrying energy from the hot region to the cold one. Turbulence therefore determines how hot a fusion plasma can get for a given heating power. Our group studies several aspects of plasma turbulence.

Understanding turbulence with interpretable machine learning

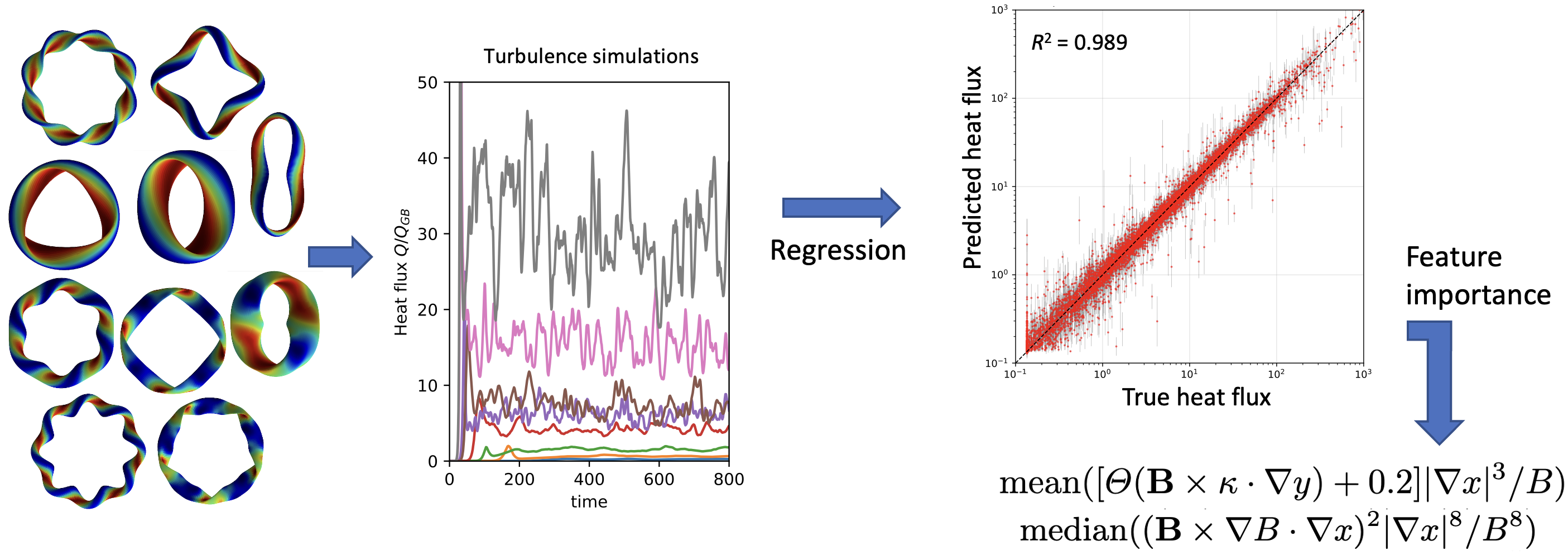
It is known that plasma turbulence depends strongly on the geometry of the magnetic field, so there is an exciting potential to increase the temperature of fusion devices by optimizing the geometry for reduced turbulence. However the details of how turbulence depends on the geometry are not clearly established. Today, it has become possible to generate large datasets of turbulence in different geometries, and machine learning (ML) methods have become available to find patterns in these datasets. In a recent publication, we demonstrated how interpretable ML methods can be used to arrive at analytic expressions involving the geometry that correlate strongly with the turbulence. The workflow for this analysis is shown in Figure 1. First, a diverse set of plasma shapes is collected. Then direct numerical simulation of the turbulence is performed in these geoemtries, using the code GX. Our dataset of over 200,000 nonlinear simulations is available online for other researchers to analyze. From each simulation we are interested in a single number: the average turbulent heat flux Q. Regressions are performed to predict Q from the geometry, taking care to respect invariances of the system. We perform millions of such regressions, comparing a combinatorial set of analytic expressions involving the geometry. Using interpretable methods such as sequential feature selection and Shapley values, we identify the geometric features with strongest correlation to the turbulence. This work shows how machine learning can be more than a black box interpolation method, by stimulating traditional physics theory and providing insights.

Subcritical turbulence

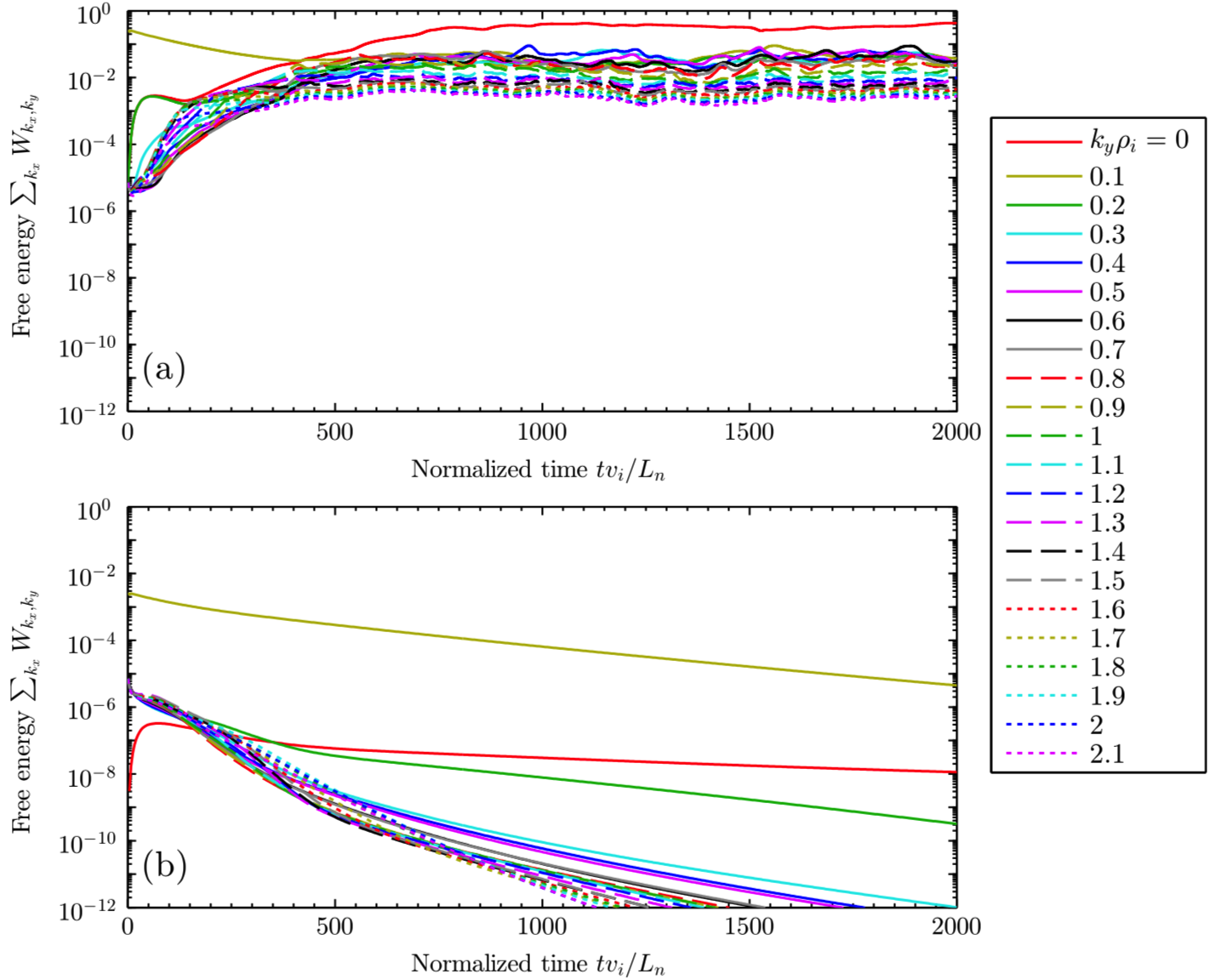
In flows of regular liquids, turbulence often is present even when linear stability analysis indicates that the laminar state should be stable. This “subcritical turbulence” is associated with shear in the flow, which allows structures to grow transiently even though their long-time linear behavior is damped. This kind of subcritical turbulence due to flow shear has also been observed in simulations of plasmas. Drake et al (1995) found that subcritical turbulence can exist in plasmas without shear in the equilibrium flow, if there is shear instead in the magnetic field, using a minimal fluid (non-kinetic) model. Our group showed that this turbulence-without-instability from magnetic shear is present also in a kinetic plasma model (“gyrokinetics”). An example is shown in figure 2: if the system is initialized with small fluctuations they decay due to linear stability, whereas if the same system is initialized with larger fluctuations, turbulence is sustained. We showed this remarkable phenomenon is associated with a discontinuous change in the system’s eigenvalues from unstable to stable as the magnetic shear is changed from zero to a finite value. Nonetheless, the plasma does not realize magnetic shear is present until particles have had time to travel sufficiently far along the field lines, giving the opportunity for large transients that can support subcritical turbulence.

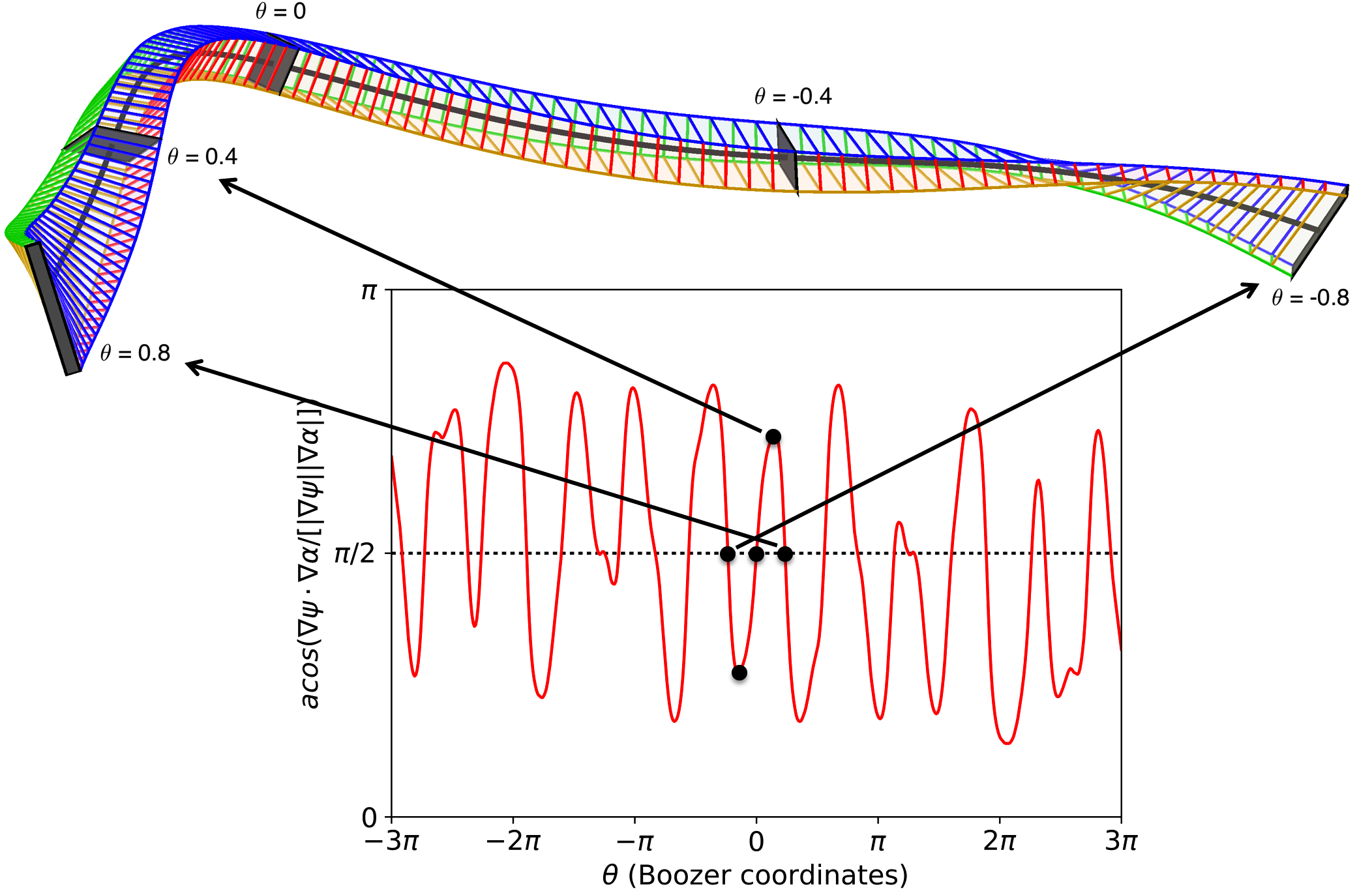
Simulating plasma turbulence in sheared magnetic fields

In magnetized plasmas, turbulence is very anisotropic, with typical fluctuation scales comparable to the gyroradii in the directions perpendicular to the magnetic field, and much longer scale lengths along the field. To model this turbulence efficiently, simulations must be carried out in “flux tubes”, elongated domains that follow the field lines. An example of a flux tube is shown in figure 3. As part of his PhD, student Mike Martin in our group developed ways to choose the shape and size of these computational domains to reduce computational cost, while preserving the accuracy of simulations. Due to the boundary conditions, the aspect ratio of the simulation domain in the two transverse directions is linked to the integrated magnetic shear along the tube. Therefore by optimizing the tube length, the ratio of the transverse dimensions can be made close to 1, minimizing the number of Fourier modes needed to resolve the turbulence. Mike showed the choice of tube length can reduce the computational cost of a W7-X turbulence simulation by a factor of 7, and the method is applicable outside of stellarators as well.